I’m off work sick today: it’s just a cold, but it’s had a damn good go at wrecking my lungs and I feel pretty lousy. You know how when you’ve got too much of a brain-fog to trust yourself with production systems but you still want to write code (or is that just me?), so this morning I threw together a really, really stupid project which you can play online here.
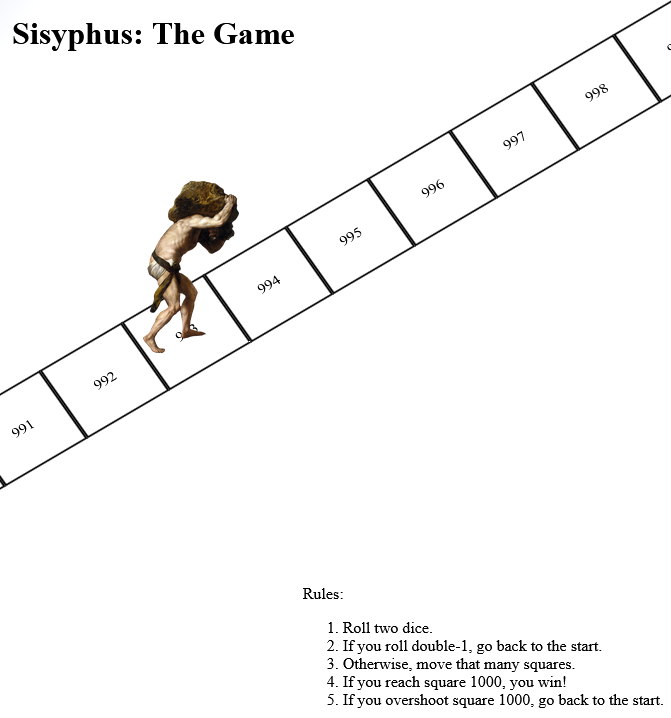
It’s inspired by a toot by Mason”Tailsteak” Williams (whom I’ve mentioned before once or twice). At first I thought I’d try to calculate the odds of winning at his proposed game, or how many times one might expect to play before winning, but I haven’t the brainpower for that in my snot-addled brain. So instead I threw together a terrible, terrible digital implementation.
Go play it if, like me, you’ve got nothing smarter that your brain can be doing today.
I won!
I cheated.
This sounds infuriating. Like the single, most drawn out way to wind up thoroughly engaged.
Ima play it later…
Read more →
@tailsteak This sounds infuriating. Like the single, most drawn out way to wind up thoroughly engaged.
Ima play it later…
My game designer brain keeps wanting to add new rules to make it more engaging, give the player(s) more control, etc, but then I remember that’s not the point.
Read more →
By crappy napkin math, it would take an average of 143 rolls to make it to 1000. Just to roll two dice 143 times without hitting a snake-eyes is a 1.78% chance. I am too lazy to compute how many of those runs you would need to land exactly on 1000, but you’ll be at it a while…
Read more →
I just noticed that you and I both misspelled “enraged” as engaged.
Read more →
Dude we already did this in Bonkers
Read more →
A few people have taken a run at the math, @digitrev actually ran 7000 simulations:
twitter.com/digitrev/statu…
Assuming you could take one turn per second, an average playthrough is about 3.5 days.
Read more →
Roll three consecutive 7s or it’s back to the torment nexus
Read more →
Riley took that to school and torment nexused her classmates.
Read more →
The goal is not to win, it’s to make others suffer just as much as you are
Read more →
The only addition I can think of would be a reminder of the option for the player to at any time accept defeat and stop rolling it. You know, to emphasize that they’re doing this to themselves.
Read more →
How DARE you bring kindness into this den of suffering.
Read more →
I also ran simulations (in Perl).
10,000 games
Best score: 160 rolls
Worse score: 1,029,702 rolls
Mean score: 112,115
Std Dev: 112,982
Not sure why my mean & std dev are 10x higher than @digitrev’s, though my worst is also 10x higher. More games = more chances for bad games.
Read more →
Exactly what I was thinking, more ways to make it more futile.
Read more →
Just for fun, ran 50,000
Best: 156
Worst: 1,402,431
Mean: 113,605
Stdev: 113,190
Definitely a long tail on the distribution — I don’t know enough stats to know if this is the best analysis.
Read more →
I probably should have looked at quartiles, since the distribution has a lower limit but not an upper limit, and even a few bad runs can drive the sample mean up crazy high
Read more →
Yeah… I did a quick histogram, the game lengths drop off quickly over 100,000, but can still go very high.
Read more →
I mean, in theory, a game could last forever.
Read more →
True. Though if it does, I recommend you have your dice checked…
Read more →
Only thing i would like to add is a highest score, nothing like the taunt of hope for having reached higher only to be brought low once again.
Read more →
I love the dice animation! Even if it’s length means I have no chance of ever completing. I wonder if anyone will ever complete this without hacking.
It’s been a while since I dusted off my statistics textbook, so I thought I’d do a proper analysis. The final results:
– The median number of turns before winning is 8995
– The expected number of turns before winning is even higher, 12930.2.
– The probability of winning if you keep at it long enough is 100%! (Statistical model does not include actuarial tables.)
I include lots of plots and explaination in a jupyter notebook which can be run on [colab][1] or downloaded from [github][2]
Thanks for the implementation!
[1]: https://colab.research.google.com/gist/sbliven/472f506c80208f8cfb74aeb4cab29b15/sisyphus.ipynb#scrollTo=eeecbc1d-5c65-4f7e-b6f9-948f1d3d503c
[2]: https://gist.github.com/sbliven/472f506c80208f8cfb74aeb4cab29b15
@tailsteak Only thing i would like to add is a highest score, nothing like the taunt of hope for having… https://t.co/XLfQPRAztK