Non-transitive Games

Non-transitive dice

Have you ever come across non-transitive dice? The classic set, that you can get in most magic shops, consists of three different-coloured six-sided dice:

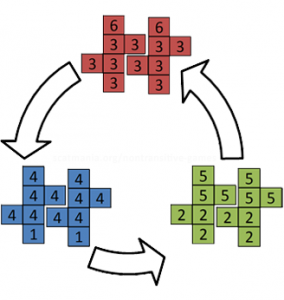
There are several variants, but a common one, as discussed by James Grime, involves one die with five “3” sides and one “6” side (described as red below), a second die with three “2” sides and three “5” sides (described as green below), and a third die with one “1” side and five “four” sides (described as blue below).

They’re all fair dice, and – like a normal six-sided dice – they all have an average score of 3.5. But they’ve got an interesting property, which you can use for all kinds of magic tricks and gambling games. Typically: the red die will beat the green die, the green die will beat the blue die, and the blue die will beat the red die! (think Rock, Paper, Scissors…)

If you want to beat your opponent, have them pick a die first. If they pick green, you take red. If they take red, you take blue. If they take blue, you take green. You now have about a 60% chance of getting the highest roll (normally you’d have about a 33% chance of winning, and a 17% chance of a draw, so a 60% chance is significantly better). To make sure that you’ve got the best odds, play “best of 10” or similar: the more times you play, the less-likely you are to be caught out by an unfortunate unlucky streak.

But if that doesn’t bake your noodle enough, try grabbing two sets of nontransitive dice and try again. Now you’ll see that the pattern reverses: the green pair tends to beat the red pair, the red pair tends to beat the blue pair, and the blue pair tends to beat the green pair! (this makes for a great second act to your efforts to fleece somebody of their money in a gambling game: once they’ve worked out how you keep winning, give them the chance to go “double or nothing”, using two dice, and you’ll even offer to choose first!)

The properties of these dice – and of the more-exotic forms, like Oskar van Deventer’s seven-dice set (suitable for playing a game with three players and beating both of your opponents) and like the polyhedral varieties discussed on Wikipedia – intrigue the game theorist and board games designer in me. Could there be the potential for this mechanic to exist in a board game? I’m thinking something with Risk-like combat (dice ‘knock out’ one another from highest to lowest) but with a “dice acquisition” mechanic (so players perform actions, perhaps in an auction format, to acquire dice of particular colours – each with their own strengths and weaknesses among other dice – to support their “hand” of dice). There’s a discussion going on in /r/tabletopgamedesign…

I’ve even written a program (which you’re welcome to download, adapt, and use) to calulate the odds of any combination of any variety of non-transitive dice against one another, or even to help you develop your own non-transitive dice sets.

Penney’s game

Here’s another non-transitive game for you, but this time: I’ve made it into a real, playable game that you can try out right now. In this game, you and I will each, in turn, predict three consecutive flips of a fair coin – so you might predict “tails, heads, heads”. Then we’ll start flipping a coin, again and again, until one of our sequences comes up. And more often than not, I’ll win.

• Play “Penney’s Game”

If you win 10 times (or you lose 20 times, which is more likely!), then I’ll explain how the game works, so you know how I “cheated”. I’ll remind you: the coin flips are fair, and it’s nothing to do with a computer – if we played this game face-to-face, with a real coin, I’d still win. Now go play!

×

×

×