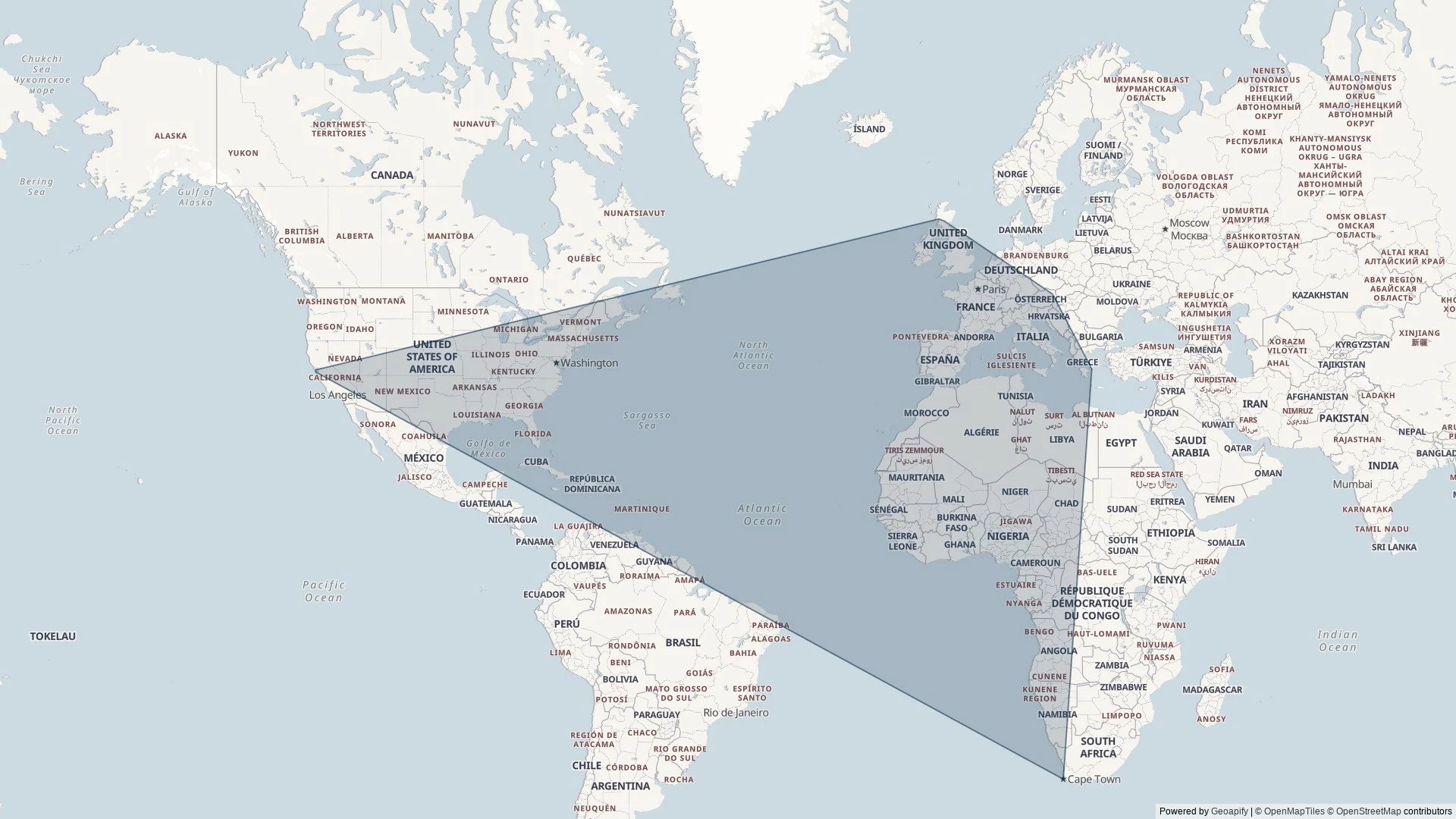
I thought it might be fun to try to map the limits of my geocaching/geohashing. That is, to draw the smallest possible convex polygon that surrounds all of the geocaches I’ve found and geohashpoints I’ve successfully visited.
Mathematically, such a shape is a convex hull – the smallest polygon encircling a set of points without concavity. Here’s how I made it:
1. Extract all the longitude/latitude pairs for every successful geocaching find and geohashpoint expedition. I keep them in my blog database, so I was able to use some SQL to fetch them:
SELECT DISTINCT coord_lon.meta_value lon, coord_lat.meta_value lat FROM wp_posts LEFT JOIN wp_postmeta expedition_result ON wp_posts.ID = expedition_result.post_id AND expedition_result.meta_key = 'checkin_type' LEFT JOIN wp_postmeta coord_lat ON wp_posts.ID = coord_lat.post_id AND coord_lat.meta_key = 'checkin_latitude' LEFT JOIN wp_postmeta coord_lon ON wp_posts.ID = coord_lon.post_id AND coord_lon.meta_key = 'checkin_longitude' LEFT JOIN wp_term_relationships ON wp_posts.ID = wp_term_relationships.object_id LEFT JOIN wp_term_taxonomy ON wp_term_relationships.term_taxonomy_id = wp_term_taxonomy.term_taxonomy_id LEFT JOIN wp_terms ON wp_term_taxonomy.term_id = wp_terms.term_id WHERE wp_posts.post_type = 'post' AND wp_posts.post_status = 'publish' AND wp_term_taxonomy.taxonomy = 'kind' AND wp_terms.slug = 'checkin' AND expedition_result.meta_value IN ('Found it', 'found', 'coordinates reached', 'Attended');
2. Next, I determine the convex hull of these points. There are an interesting variety of algorithms for this so I adapted the Monotone Chain approach (there are convenient implementations in many languages). The algorithm seems pretty efficient, although that doesn’t matter much to me because I’m caching the results for a fortnight.
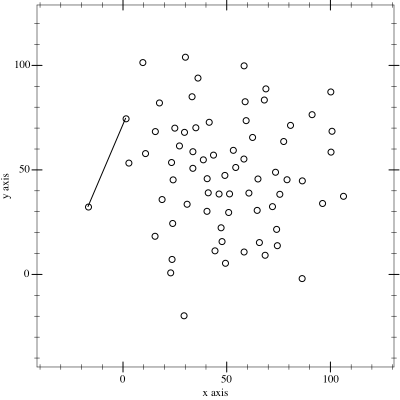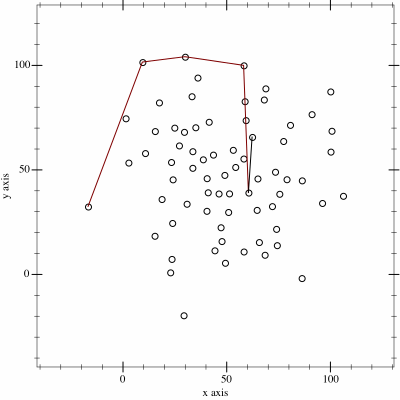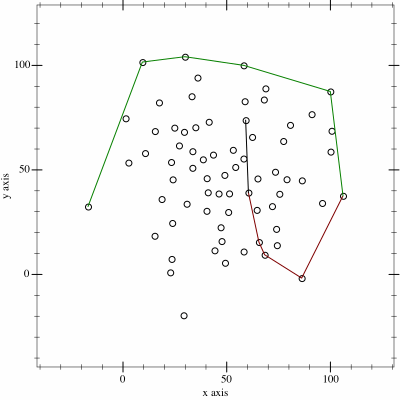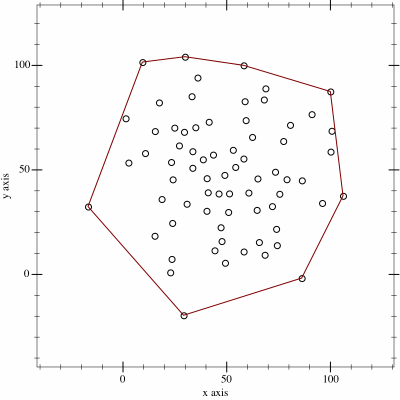
3. Finally, I push the hull coordinates into Geoapify, who provide mapping services to me. My full source code is available.
An up-to-date (well, no-more than two weeks outdated) version of the map appears on my geo* stats page. I don’t often get to go caching/hashing outside the bounds already-depicted, but I’m excited to try to find opportunities to push the boundaries outwards as I continue to explore the world!
(I could, I suppose, try to draw a second larger area of places I’ve visited: the difference between the smaller and larger areas would represent all of the opportunities I’d missed to find a hashpoint!)
Oh this is super cool!
I once did something similar for places visited, just by manually drawing it out on Google earth. Did the same for some friends too, but it got tricky to define for my sister who works as cabin crew…
Once the points cover most the globe it’s weird to define which side is inside and which is outside? Especially when doing it on a sphere…
I like the convex hull algorithm too, I had never gotten as far as finding one of those, definitely fascinating to watch.. I’m eager to try and build something that implements it now.
Seems like there’s a fair few opportunities to grow your polygon there though! Wishing you good adventures!
Would certainly be cool to see the missed opportunities polygon too :D
By the time I were getting circumnavigational I might do the “hard maths” to translate altitude, or sea level if unknown, into a three-dimensional coordinate space and use one of the 3D variants of the convex hull algorithm (it turns out that it can under some circumstances be an entirely different order of problem!), and try to express it as a 3D space.
If I were feeling especially brave, I might even try to represent my “finds” over time in a 4D spacetime model! Though I’ve no idea how the visualisation of that might work…
See now this gives me a whole new angle (lol) for trying to convince you to travel to places. It won’t help me get you to go to Liechentstein but British Columbia or Patagonia look really promising right now…
I might do as Tulip nudged and put a super-hull of places I know I’ve travelled to show a “missed opportunities” map. Might need to do some research first to remember all the places I’ve been! While I’m pretty good at tracking my location, my data begins to peter out from about a decade ago and complete vanishes within two, and there’s plenty of interesting places I know I’ve been to that won’t show up unless I do some manual curation…
…Iceland, New Zealand…
Tokyo, maybe?
As suggested/requested in the comments above, I’ve made a map which contains a “super-hull” showing the absolute limits of places where I’ve been (must have stood on the ground: e.g. polar flights don’t count). The area between the inner and outer polygons is my “space of missed opportunities” to geocache/geohash (although it’s gotta be said that I visited some of those places before either sport was invented!):
It’s a good thing I’m not reading this at a computer, or I’d be at serious risk of being nerd sniped.
As it is, I’m wondering about the correct variant of this problem on a sphere. The 2d hull on a projection is problematic (even setting aside the problem of wrapping around the hemispheres) because the perimeter lines should be great circles and map distortion could give bad results.
“Convex” doesn’t have a consistent definition on a curved surface, so I’m not sure how the convex hull would be computed on a sphere.
One option is to find the smallest spherical cap containing all points. This is well defined, but would tend to be considerably bigger than the “hull” and might only touch e two or three points.
Maybe we need to go fully 3D? Any set of points on a sphere define a convex polyhedron. Maybe you get bragging rights depending on how close to the volume of the earth your polyhedron fills.
I know how to make that map even more interesting 😜
Some amalgamated stats on my geocaching/geohashing activity, regardless of the site it was originally posted on (thanks to this): The area in which I’ve geocached/geohashed can be drawn as a 2D convex hull (up-to-date as of April 2024):
Read more →