What have I been up to of late? Well, as you ask…
Diplomacy
Ruth‘s game of Diplomacy got off to a fine start, and the backstabbing began soon afterwards. I’m not so keen on the engine, for reasons I’ll discuss later. Here’s how the map looks right now.
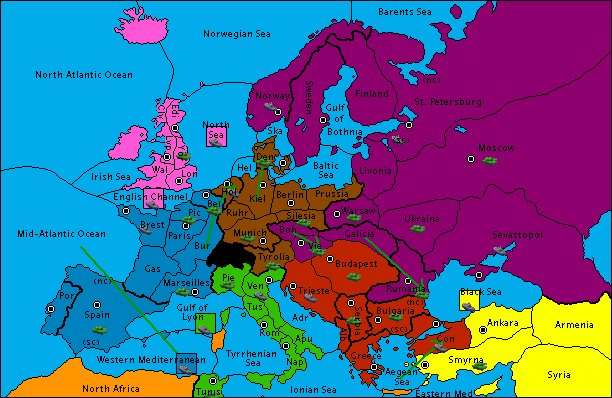
I’m the red guys down at the bottom who are getting their arses kicked by the purple and brown guys. Very sweetly, JTA (leader of Russia) sent me an e-mail to apologise a little (and gloat a lot) about his recent pillaging of my lands, and congratulate me on trying to set him and Andy (Germany) against one another. It’s kind-of sweet, as I said, but really un-necessary: breaking alliances is what the game is all about.
Plus, it’s not like I didn’t see it coming. My alliance with Russia as a show from the start, but I didn’t realise that Russia planned to attack me so soon (I’d just issued attack orders against him). My mistake was that I didn’t anticipate that Germany side with Russia and backstab me. Memo to self: assassinate leader of Germany.
Sadly, the Diplomacy engine we’re using – phpDiplomacy – has a few interesting bugs that make it hard to work out who’s actually on your side. Here’s an example situation:
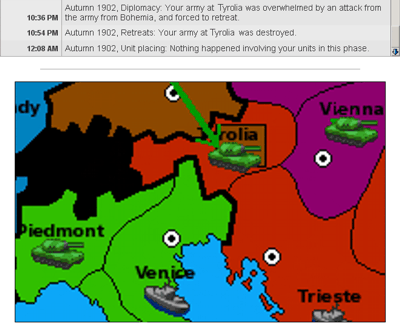
The screenshot is faked, but the situation is plausible – the engine doesn’t accomodate for this. In this situation, the red player has been successfully attacked by the brown player, displacing their army (according to the message from 10:36pm). It’s not possible that the brown player did this alone, in this situation: they must have had help from at least one of – the green army in Piedmont, the green fleet in Venice, the purple army in Vienna, possibly a purple army from the region above (not shown), or perhaps even from the red fleet in Trieste (an unusual strategy, but not unheard of in some unusual circumstances, is to support the enemy against your own units).
But the engine gives no indication which this is. In this situation, the red player does not know which – green or purple – supported the attack. If the red player had alliances with the two of them, they would not know which one had betrayed them, for example. Whoops!
This could make it an interesting (or a frustrating) game. I’m certain that in the near future we’ll see players strategically helping one another perform attacks, without revealing that it was them that supported it.
A Strange Parcel

This morning, I received a strange parcel from Matt in the Hat, addressed to “Jen, Paul, Dan & Claire”. The contents, as pictured, seem to be two Guinness glasses and three cartons of organic fruit juice. I’m not sure which bits are for whom – or even why we’ve been sent this package at all – but I’m sure Matt will enlighten me soon.
Update: I’ve spoken to Matt on Jabber, and apparently the Guinness glasses box does not contain Guinness glasses. And I’m to make sure that Jen gets one of the cartons of juice.
Basically, Matt’s lost the plot. However, he still managed, through his insanity, to pick a selection of objects who’s size ratios made packing them easy.
Company of Heroes
I’ve been playing a lot of Company of Heroes these last couple of days: it’s a spectacular game. It’s been a long time since a real-time strategy game has amused me so much (since, perhaps Red Alert 2, seven years ago). It’s yet-another-world-war-2 game, as if we haven’t seen enough of them of late, but it’s a battle-level strategic game, rather than a first-person shooter, and it does a wonderful job of what it does.
Tanks roll through deformable terrain. Infantry hide in the craters your artillery has blown out. And the whole thing looks and sounds beautiful, from the hushed descent of paratroopers into a muddy field (reflections and all) to the flashes and blasts of a distant battle (complete with radio chatter, or plain old voices if you’re looking directly at the speaker). You can build sandbag walls and minefields, and blow them down just as easily. Don’t want to risk your men down a long, sniper-infested street? Steal some German artillery pieces and blow your way though the walls, then – the whole map is completely reshapable. The AI’s not to be sniffed at, either (although it’s a bit fiddly when it comes to multi-selecting and moving a group of vehicles together and they all crumple into each other when they reach a chicane, rather than taking turns).
It needs a beefy machine to do it justice, which is why I got it – to push my new gaming rig to the limits – but it’s more than just a graphics-fest: it’s also a very clever and gritty game.
So, who’s for a co-op?
Writing Comedy
And, of course, the other thing that’s been occupying my time has been writing stuff to say on Sunday’s Gorillamania event. But I’ve already said enough about that recently, so I’ll shut up and get on with some work.