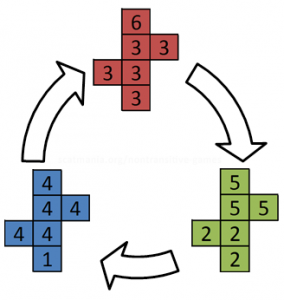
I was having trouble visualising the dice probabilities for some Forged in the Dark-based1 RPGs2, so I drew myself a diagram. I don’t know who, if anybody, would be interested in such a thing other than me… but that’s why we put these things online, right?
The general idea for Forged in the Dark action resolution is that you throw a number of six-sided dice representative of your chance of success3. You look at the highest value rolled in your dice pool, typically with most or all of the following effects:
- 1-3: Failure – depending on the circumstances you might be able to try again (with greater risk) and/or suffer some kind of consequence (a “harm” or “complication”).
- 4-5: Limited success – you succeed, but with come kind of consequence.
- 6: Success – you succeed!
- Multiple 6s: Critical – you succeed, and it’s more-effective than you’d hoped or you gain some other benefit4.
If you’re playing Blades in the Dark or another Forged in the Dark-based game and find it useful to visualise how likely you are to get screwed-over by the dice… you’re welcome!
Footnotes
1 Forged in the Dark is the name of the permissively-licensed SRD originally used for fantasy RPG Blades in the Dark, but it’s been used in plenty of other places too where its relatively fast-and-loose mechanics are best-suited. Sharp-eyed readers might have noticed this come up in a repost from last week, too…
2 I may or may not be considering Forged in the Dark as the engine for a prototype RPG environment I’ve been half-heartedly constructing this winter…
3 A task for which you’ve prepared and have trained, in an area in which you’re skilled, and for which you’re well-equipped (e.g. an accomplished thief takes the time to carefully pick a basic lock using fine tools) is likely to involve rolling more dice than a less-fortunate individual.
4 I’m hugely grateful to AnyDice for helping with these calculations. Did you know that you need to be rolling ten six-sided dice before it becomes more-likely-than-not that there’ll be a double-six somewhere in there?